
Standard form is a shorthand way of expressing VERY LARGE or VERY SMALL numbers. There are 6 key skills that you need to learn.
Standard from to ordinary numbers and ordinary numbers to standard form are two skills you will be taught.
Make sure you are happy with the following topics before continuing:

We always write a number in standard form exactly like this:
The Three Key Rules
2) Standard form is always \textcolor to the power of something ( \textcolor )
3) \textcolor must be a whole number, this is the number of places the decimal point moves .
e.g. \textcolor\times\textcolor^\textcolor
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSE 
Example: Express 4.2\times\textcolor as a number not in standard form .
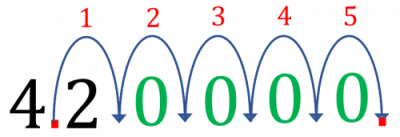

Then, we get 4.2\times10^5=4.2\times10\times10\times10\times10\times10
Multiplying by 10 means moving the decimal place to the right, here we must do it 5 times:
Step 1: Write 4\textcolor<.>2 out and move the decimal place \textcolor jumps to the right.
Step 2: Add \textcolor<\mathbf<0>> ‘s to fill in the spaces created as the decimal point has moved.
Step 3: Remove the original decimal point .
This gives the answer to be:
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSE 
Example: Write 2.8\times\textcolor> in decimal notation.
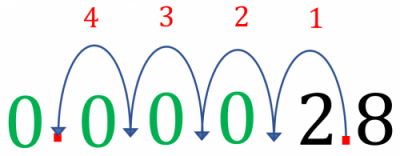

This is different because the power is negative, but it’s actually no harder. We know,
This means we are \textcolor10> \textcolor> which means we move the decimal point 4 spaces to the left.
Step 1: Write 2\textcolor<.>8 out and move the decimal place \textcolor jumps to the left.
Step 2: Add \textcolor<\mathbf<0>> ‘s to fill in the space created as the decimal point has moved.
Step 3: Remove the original decimal point .
Therefore, we have concluded that
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSE Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEExample: Write 56,700,000 in standard form .
Step 1: Move the decimal point to the left until the number becomes 5.67 (1\leq A<10)
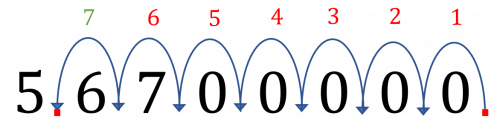
Step 2: Count the number of times the decimal point has moved to the left, this will become our power ( \textcolor ), in this case \textcolor .
Step 3: We have moved to the left meaning it will be \textcolor not -7
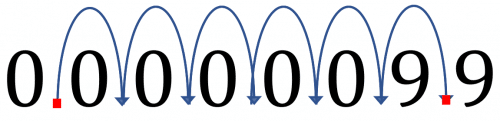
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEExample: Write 0.0000099 in standard form .
Step 1: Move the decimal point to the right until the number becomes 9.9 (1\leq A<10)
Example: Find the standard form value of (3\times10^8)\times(7\times10^4) , without using a calculator.
Step 1: Change the order around of the things being multiplied.
Step 2: Multiply the numbers and the powers out separately.
Step 3: Convert the number at the front to standard form if necessary ( 1 \leq A < 10 ).
This answer is not in standard form ( 21 is not between 1 and 10 ), and we need it to be. Fortunately, if we recognise that \textcolor=\textcolor\textcolor , then we get that
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEExample: Find the standard form value of (\textcolor\times\textcolor>)\div(\textcolor\times\textcolor) , without using a calculator.
Step 1: Break up the problem and change the order of how we divide things.
Step 2: Convert the number at the front to standard form if necessary ( 1 \leq A < 10 ).
\textcolor is between 1 and 10 , so this answer is in standard form, and so we are done.
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEQuestion 1: What is 1.15\times10^ in decimal notation?
[1 mark]
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEThe power is negative, so this is going to be a very small number. As the power of ten is -6 , we want to divide the number 1.15 by 10 six times, and so we will move the decimal point six places to the left.

Save your answers with
Gold Standard Education
Show Answer Still marking manually? Save your answers withFind out more
Question 2: What is 5,980,000 in standard form?
[1 mark]
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEIn this case, the power of 10 is going to be positive.
So, if we move the decimal point in 5,980,000 to the left six places it becomes 5.98 . Therefore, we get that,

Save your answers with
Gold Standard Education
Show Answer Still marking manually? Save your answers withFind out more
Question 3: What is 0.0068 in standard form?
[1 mark]
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEBy considering the position where the first non-zero digit is compared to the units column we find,
as the 6 is 3 places away from the units column.

Save your answers with
Gold Standard Education
Show Answer Still marking manually? Save your answers withFind out more
Question 4: Calculate 5,600,000\div800
Give your answer in standard form.
[3 marks]
Level 4-5 GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEFirst, write each of the numbers in standard form i.e. 5.6\times10^6 and 8\times10^2
Using the formula 10^a\div10^b=10^ we can rewrite the eqaution as,
Standard form requires the number be between 1 and 10 , so adjusting by a factor of 10 , we have,

Save your answers with
Gold Standard Education
Show Answer Still marking manually? Save your answers withFind out more
Question 5: Calculate (2.5\times10^)\times(6\times10^) .
Give your answer in standard form.
[3 marks]
GCSE KS3 AQA Edexcel OCR WJEC Cambridge iGCSE Edexcel iGCSEWe will split up this multiplication, multiplying the initial numbers together and the powers of 10 together separately. Firstly,
Secondly, using the multiplication law of indices,
(2.5\times10^)\times(6\times10^) =2.5\times6\times10^4\times10^\\ =15\times10^
Standard form requires the number be between 1 and 10 , so adjusting by a factor of 10 , we have,

Save your answers with
Gold Standard Education