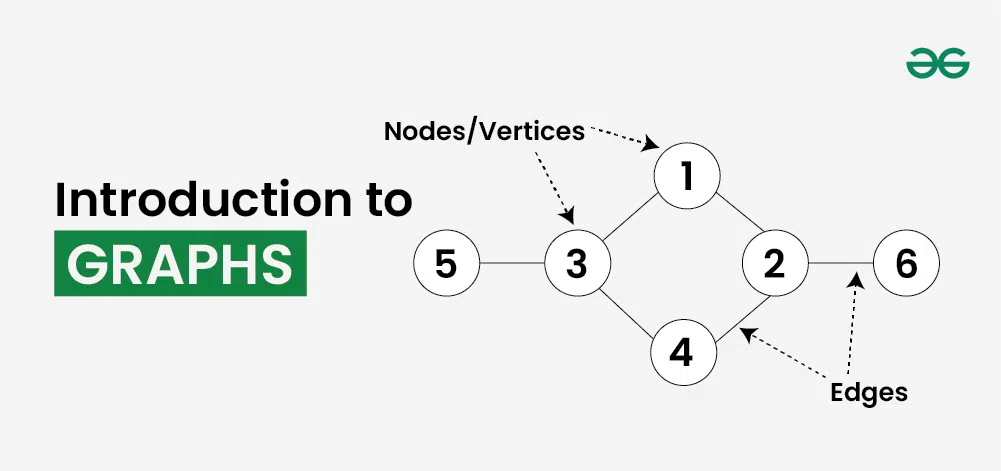
Graph Data Structure is a non-linear data structure consisting of vertices and edges. It is useful in fields such as social network analysis, recommendation systems, and computer networks. In the field of sports data science, graph data structure can be used to analyze and understand the dynamics of team performance and player interactions on the field.

Table of Content
Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E).
Imagine a game of football as a web of connections, where players are the nodes and their interactions on the field are the edges. This web of connections is exactly what a graph data structure represents, and it’s the key to unlocking insights into team performance and player dynamics in sports.
A graph is known as a null graph if there are no edges in the graph.
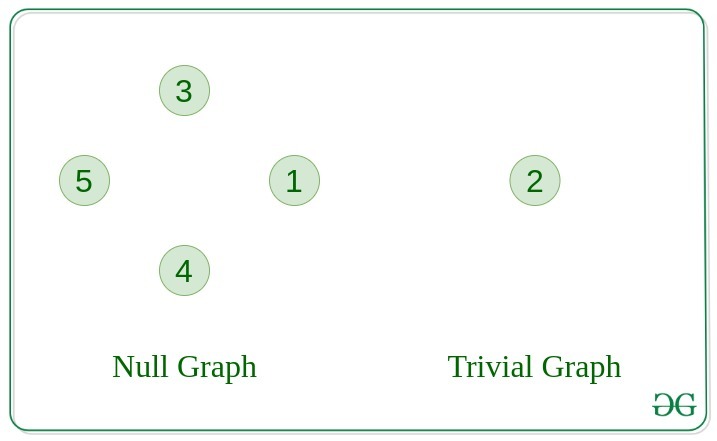
Graph having only a single vertex, it is also the smallest graph possible.
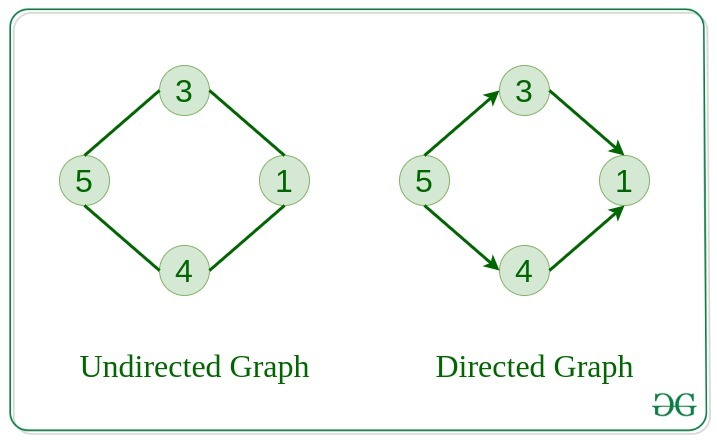
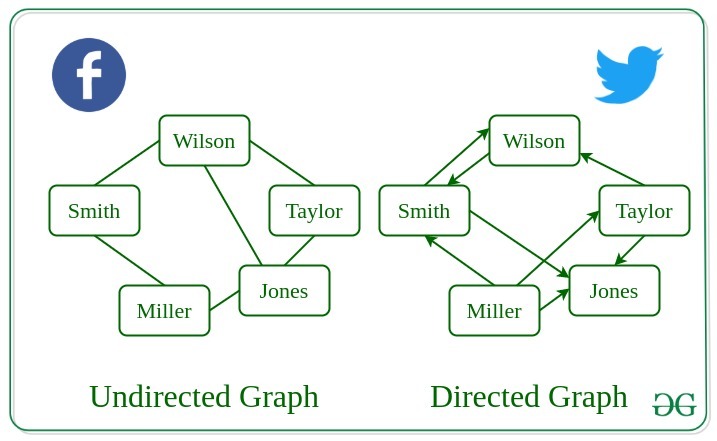
A graph in which edges do not have any direction. That is the nodes are unordered pairs in the definition of every edge.
A graph in which edge has direction. That is the nodes are ordered pairs in the definition of every edge.
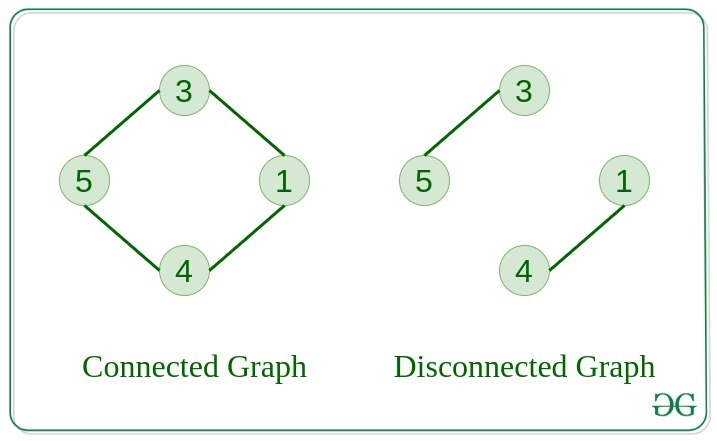
The graph in which from one node we can visit any other node in the graph is known as a connected graph.
The graph in which at least one node is not reachable from a node is known as a disconnected graph.
The graph in which the degree of every vertex is equal to K is called K regular graph.
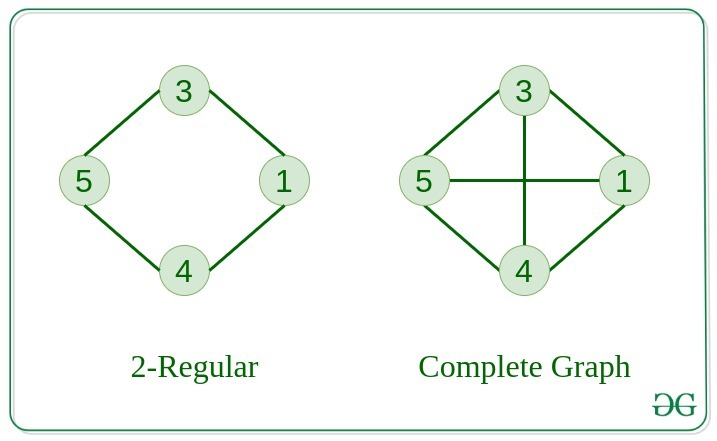
The graph in which from each node there is an edge to each other node.
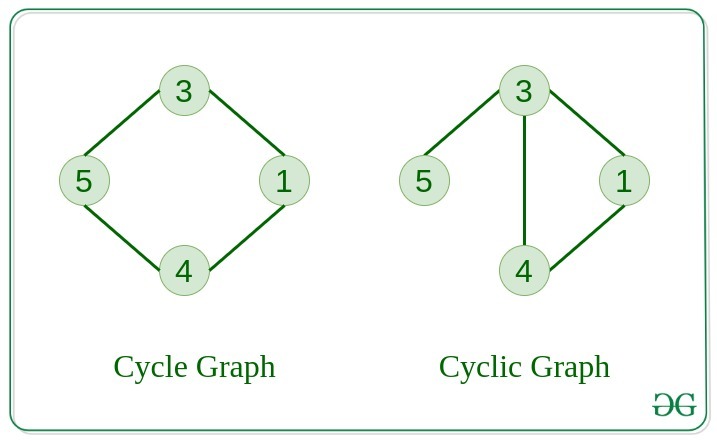
The graph in which the graph is a cycle in itself, the minimum value of degree of each vertex is 2.
A graph containing at least one cycle is known as a Cyclic graph.
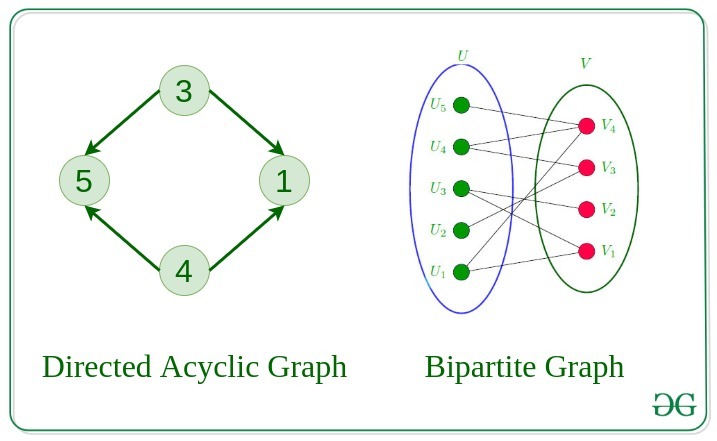
A Directed Graph that does not contain any cycle.
A graph in which vertex can be divided into two sets such that vertex in each set does not contain any edge between them.
There are multiple ways to store a graph: The following are the most common representations.
In this method, the graph is stored in the form of the 2D matrix where rows and columns denote vertices. Each entry in the matrix represents the weight of the edge between those vertices.
-copy.webp)
Below is the implementation of Graph Data Structure represented using Adjacency Matrix:
> mat = , , , >; */ C
, , , ; */ Java
, , , >; */ Python
, , , ; JavaScript
Adjacency Matrix Representation 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 0
This graph is represented as a collection of linked lists. There is an array of pointer which points to the edges connected to that vertex.
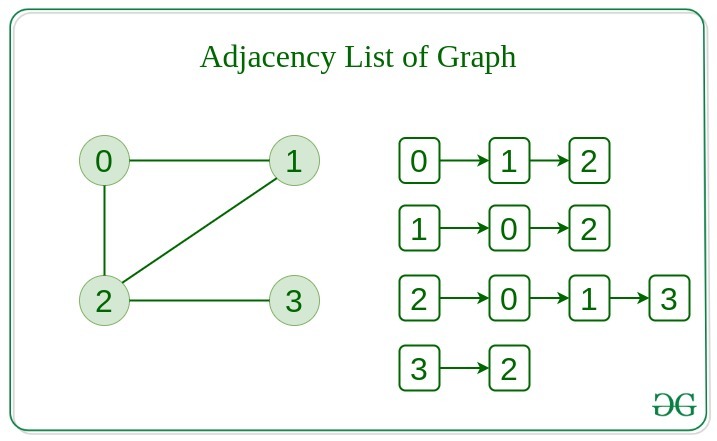
Below is the implementation of Graph Data Structure represented using Adjacency List:
Java
Python
JavaScript
Adjacency List Representation: 0: 1 2 1: 0 2 2: 0 1 3 3: 2
When the graph contains a large number of edges then it is good to store it as a matrix because only some entries in the matrix will be empty. An algorithm such as Prim’s and Dijkstra adjacency matrix is used to have less complexity.
| Action | Adjacency Matrix | Adjacency List |
|---|---|---|
| Adding Edge | O(1) | O(1) |
| Removing an edge | O(1) | O(N) |
| Initializing | O(N*N) | O(N) |
Below are the basic operations on the graph:
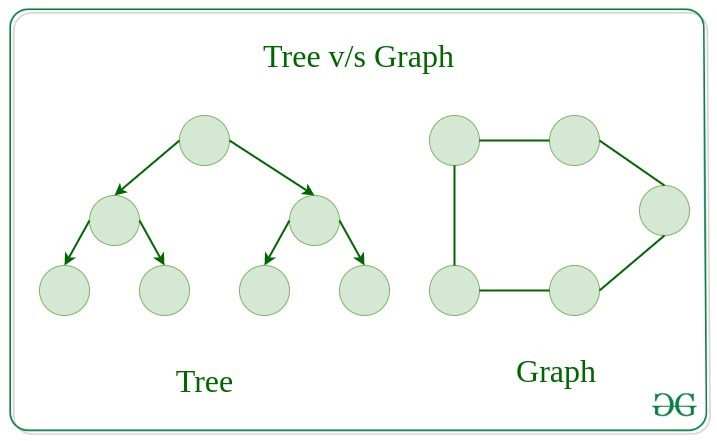
Tree is a restricted type of Graph Data Structure, just with some more rules. Every tree will always be a graph but not all graphs will be trees. Linked List , Trees , and Heaps all are special cases of graphs.
Graph Data Structure has numerous real-life applications across various fields. Some of them are listed below:
A graph is a data structure consisting of a set of vertices (nodes) and a set of edges that connect pairs of vertices.
Graph Data Structure can be classified into various types based on properties such as directionality of edges (directed or undirected), presence of cycles (acyclic or cyclic), and whether multiple edges between the same pair of vertices are allowed (simple or multigraph).
Graph Data Structure has numerous applications in various fields, including social networks, transportation networks, computer networks, recommendation systems, biology, chemistry, and more.
In an undirected graph, edges have no direction, meaning they represent symmetric relationships between vertices. In a directed graph (or digraph), edges have a direction, indicating a one-way relationship between vertices.
A weighted graph is a graph in which each edge is assigned a numerical weight or cost. These weights can represent distances, costs, or any other quantitative measure associated with the edges.
The degree of a vertex in a graph is the number of edges incident to that vertex. In a directed graph, the indegree of a vertex is the number of incoming edges, and the outdegree is the number of outgoing edges.
A path in a graph is a sequence of vertices connected by edges. The length of a path is the number of edges it contains.
A cycle in a graph is a path that starts and ends at the same vertex, traversing a sequence of distinct vertices and edges in between.
A spanning tree of a graph is a subgraph that is a tree and includes all the vertices of the original graph. A minimum spanning tree (MST) is a spanning tree with the minimum possible sum of edge weights.
Common graph traversal algorithms include depth-first search (DFS) and breadth-first search (BFS). These algorithms are used to explore or visit all vertices in a graph, typically starting from a specified vertex. Other algorithms, such as Dijkstra’s algorithm and Bellman-Ford algorithm, are used for shortest path finding.